Learning is an inherent characteristic of the human beings. By virtue of this,
people, while executing similar tasks, acquire the ability to improve their
performance. This chapter provides an overview of the principle of learning
that can be adhered to machines to improve their performance. Such learning
is usually referred to as ‘machine learning’. Machine learning can be broadly
classified into three categories: i) Supervised learning, ii) Unsupervised
learning and iii) Reinforcement learning. Supervised learning requires a trainer, who supplies the input-output training instances. The learning system
adapts its parameters by some algorithms to generate the desired output
patterns from a given input pattern. In absence of trainers, the desired output
for a given input instance is not known, and consequently the learner has to
adapt its parameters autonomously. Such type of learning is termed
‘unsupervised learning’. The third type called the reinforcement learning
bridges a gap between supervised and unsupervised categories. In
reinforcement learning, the learner does not explicitly know the input-output
instances, but it receives some form of feedback from its environment. The
feedback signals help the learner to decide whether its action on the
environment is rewarding or punishable. The learner thus adapts its
parameters based on the states (rewarding / punishable) of its actions. Among
the supervised learning techniques, the most common are inductive and
analogical learning. The inductive learning technique, presented in the
chapter, includes decision tree and version space based learning. Analogical
learning is briefly introduced through illustrative examples. The principle of
unsupervised learning is illustrated here with a clustering problem. The
section on reinforcement learning includes Q-learning and temporal difference
learning. A fourth category of learning, which has emerged recently from the
disciplines of knowledge engineering, is called ‘inductive logic
programming’. The principles of inductive logic programming have also been
briefly introduced in this chapter. The chapter ends with a brief discussion on
the ‘computational theory of learning’. With the background of this theory,
one can measure the performance of the learning behavior of a machine from
the training instances and their count.
As already mentioned, in supervised learning a trainer submits the inputoutput
exemplary patterns and the learner has to adjust the parameters of the
system autonomously, so that it can yield the correct output pattern when
excited with one of the given input patterns. We shall cover two important
types of supervised learning in this section. These are i) inductive learning and
ii) analogical learning.
In supervised learning we have a set of {xi, f (xi)} for 1≤i≤n, and our aim is
to determine ‘f’ by some adaptive algorithm. The inductive learning is
a special class of the supervised learning techniques, where given a set of {xi,
f(xi)} pairs, we determine a hypothesis h(xi ) such that h(xi )≈f(xi ), ∀ i. A
natural question that may be raised is how to compare the hypothesis h that
approximates f. For instance, there could be more than one h(xi ) where all of
which are approximately close to f(xi ). Let there be two hypothesis h1 and h2,
where h1(xi) ≈ f(xi) and h2(xi) = f(xi). We may select one of the two
hypotheses by a preference criterion, called bias.
When {xi, f(xi)}, 1≤ ∀i ≤ n are numerical quantities we may employ the
neural learning techniques presented in the next chapter. Readers may
wonder: could we find ‘f’ by curve fitting as well. Should we then call curve
fitting a learning technique? The answer to this, of course, is in the negative.
The learning algorithm for such numerical sets {xi, f(xi )} must be able to
adapt the parameters of the learner. The more will be the training instance, the
larger will be the number of adaptations. But what happens when xi and f(xi)
are non-numerical? For instance, suppose given the truth table of the
following training instances.
Truth Table: Training Instances

Here we may denote bi = f (ai, ai→bi) for all i=1 to n. From these training
instances we infer a generalized hypothesis h as follows.
In inductive learning we observed that there exist many positive and negative
instances of a problem and the learner has to form a concept that supports
most of the positive and no negative instances. This demonstrates that a
number of training instances are required to form a concept in inductive
learning. Unlike this, analogical learning can be accomplished from a single
example. For instance, given the following training instance, one has to
determine the plural form of bacilus.
Obviously, one can answer that the plural form of bacillus is bacilli. But
how do we do so? From common sense reasoning, it follows that the result is
because of the similarity of bacillus with fungus. The analogical learning
system thus learns that to get the plural form of words ending with ‘us’ is to
replace it with ‘i’.
The main steps in analogical learning are now formalized below.
- Identifying Analogy: Identify the similarity between an
experienced problem instance and a new problem. - Determining the Mapping Function: Relevant parts of the
experienced problem are selected and the mapping is
determined. - Apply Mapping Function: Apply the mapping function to
transform the new problem from the given domain to the target
domain. - Validation: The newly constructed solution is validated for its
applicability through its trial processes like theorem or
simulation. - Learning: If the validation is found to work well, the new
knowledge is encoded and saved for future usage.
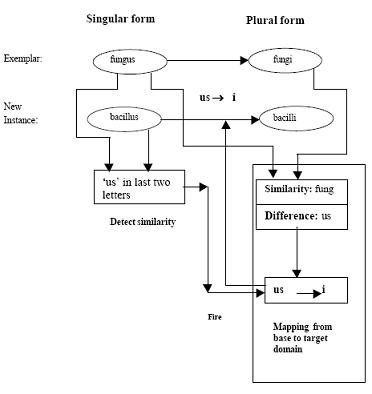
Learning from an example.
Analogical reasoning has been successfully realized in many systems.
Winston’s analogical system was designed to demonstrate that the
relationship between acts and actors in one story can explain the same in
another story. Carbonell’s transformational analogy system employs a new
approach to problem solving. It solves new problems by modifying existing
solutions to problems until they may be applied to new problem instances.
