Introduction to Artificial Intelligence
Defining Artificial Intelligence
The phrase “Artificial Intelligence” was first coined by John McCarthy four decades ago. One representative definition is pivoted around comparing intelligent machines with human beings. Another definition is concerned with the performance of machines which historically have been judged to lie within the domain of intelligence.
Yet none of these definitions have been universally accepted, probably because the reference of the word “intelligence” which is an immeasurable quantity. A better definition of artificial intelligence, and probably the most accurate would be: An artificial system capable of planning and executing the right task at the right time rationally. Or far simpler: a machine that can act rationally.
With all this a common questions arises:
Does rational thinking and acting include all characteristics of an intelligent system?
If so, how does it represent behavioral intelligence such as learning, perception and planning?
If we think a little, a system capable of reasoning would be a successful planner. Moreover, a system can act rationally only after acquiring knowledge from the real world. So the property of perception is a perquisite of building up knowledge from the real world.
With all this we may conclude that a machine that lacks of perception cannot learn, therefore cannot acquire knowledge.
General Problem Solving Approaches in AI
To understand the practical meaning or “artificial intelligence” we must illustrate some common problems. All problems that are dealt with artificial intelligence solutions use the common term “state”.
A state represents the status of a solution at a given step during the problem solving procedure. The solution of a problem is a collection of “states”. The problem solving procedure or algorithm applies an operator to a “state” to get the next state. Then, it applies another operator to the resulting state to derive a new state.
The process of applying operators to each state is continued until a desired goal is achieved.
Example : Consider a 4-puzzle problem, where in a 4-cell board there are 3 cells filled with digits and 1 blank cell. The initial state of the game represents a particular orientation of the digits in the cells and the final state to be achieved is another orientation supplied to the game player. The problem of the game is to reach from the given initial state to the goal (final) state, if possible, with a minimum of moves. Let the initial and the final state be as shown in figures 1(a) and (b) respectively.

Fig.: The initial and the final states of the Number Puzzle game, where B denotes the blank space.
We now define two operations, blank-up (BU) / blank-down (BD) and blank-left (BL) / blank-right (BR), and the state-space (tree) for the problem is presented below using these operators. The algorithm for the above kind of problems is straightforward. It consists of three steps, described by steps 1, 2(a) and 2(b) below.
Algorithm for solving state-space problems
Begin
- state: = initial-state; existing-state:=state;
- While state ≠ final state do
Begin- a. Apply operations from the set {BL, BR, BU, BD} to each state so as to generate new-states;
- b. If new-states ∩ the existing-states ≠ φ
- Begin state := new-states - existing-states;
- Existing-states := existing-states - {states}
- End;
- End while;
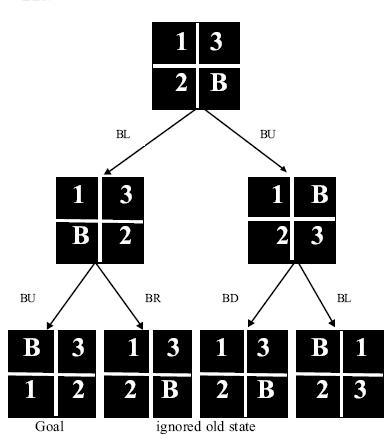
Fig.: The state-space for the Four-Puzzle problem.
It is clear that the main trick in solving problems by the state-space approach is to determine the set of operators and to use it at appropriate states of the problem.
Researchers in artificial intelligence have segregated the AI problems from the non-AI problems. Generally, problems, for which straightforward mathematical / logical algorithms are not readily available and which can be solved by intuitive approach only, are called AI problems.
The 4-puzzle problem, for instance, is an ideal AI Problem. There is no formal algorithm for its realization, i.e., given a starting and a goal state, one cannot say prior to execution of the tasks the sequence of steps required to get the goal from the starting state. Such problems are called the ideal AI problems.
The well known water-jug problem, the Traveling Salesperson Problem (TSP), and the n-Queen problem are typical examples of the classical AI problems.
Among the non-classical AI problems, the diagnosis problems and the pattern classification problem need special mention. For solving an AI problem, one may employ both artificial intelligence and non-AI algorithms. An obvious question is: what is an AI algorithm?
AI Algorithm
Formally speaking, an artificial intelligence algorithm generally means a non-conventional intuitive approach for problem solving. The key to artificial intelligence approach is intelligent search and matching. In an intelligent search problem / sub-problem, given a goal (or starting) state, one has to reach that state from one or more known starting (or goal) states.
For example, consider the 4-puzzle problem, where the goal state is known and one has to identify the moves for reaching the goal from a pre-defined starting state. Now, the less number of states one generates for reaching the goal, the better. That is the AI algorithm.
The question that then naturally arises is: how to control the generation of states?
This can be achieved by suitably designing control strategies, which would filter a few states only from a large number of legal states that could be generated from a given starting / intermediate state.
As an example, consider the problem of proving a trigonometric identity that children are used to doing during their schooldays. What would they do at the beginning? They would start with one side of the identity, and attempt to apply a number of formula there to find the possible resulting derivations.
But they won’t really apply all the formula there. Rather, they identify the right candidate formula that fits there, such that the other side of the identity that seems to be closer in some sense (outlook). Ultimately, when the decision regarding the selection of the formula is over, they apply it to one side (say the L.H.S) of the identity and derive the new state.
Therefore, they continue the process and go on generating new intermediate states until the R.H.S (goal) is reached. But do they always select the right candidate formula at a given state? From our experience, we know the answer is “not always”. But what would we do if we find that after generation of a few states, the resulting expression seems to be far away from the R.H.S of the identity.
Perhaps we would prefer to move to some old state, which is more promising, i.e., closer to the R.H.S of the identity. The above line of thinking has been realized in many intelligent search problems of AI.
Some of these well-known search algorithms are:
- Generate and Test
- Hill Climbing
- Heuristic Search
- Means and Ends analysis
a) Generate and Test Approach : This approach concerns the generation of the state-space from a known starting state (root) of the problem and continues expanding the reasoning space until the goal node or the terminal state is reached.
In fact after generating each and every state, the generated node is compared with the known goal state. When the goal is found, the algorithm terminates. In case there exist multiple paths leading to the goal, then the path having the smallest distance from the root is preferred. The basic strategy used in this search is only generation of states and their testing for goals but it does not allow filtering of states.
(b) Hill Climbing Approach : Under this approach, one has to first generate a starting state and measure the total cost for reaching the goal from the given starting state. Let this cost be f. While f = a predefined utility value and the goal is not reached, new nodes are generated as children of the current node. However, in case all neighborhood nodes (states) yield an identical value of f and the goal is not included in the set of these nodes, the search algorithm is trapped at a hillock or local extreme.
One way to overcome this problem is to select randomly a new starting state and then continue the above search process. While proving trigonometric identities, we often use Hill Climbing, perhaps unknowingly.
(c) Heuristic Search: Classically heuristics means rule of thumb. In heuristic search, we generally use one or more heuristic functions to determine the better candidate states among a set of legal states that could be generated from a known state.
The heuristic function, in other words, measures the fitness of the candidate states. The better the selection of the states, the fewer will be the number of intermediate states for reaching the goal.
However, the most difficult task in heuristic search problems is the selection of the heuristic functions. One has to select them intuitively, so that in most cases hopefully it would be able to prune the search space correctly.
(d) Means and Ends Analysis: This method of search attempts to reduce the gap between the current state and the goal state. One simple way to explore this method is to measure the distance between the current state and the goal, and then apply an operator to the current state, so that the distance between the resulting state and the goal is reduced. In many mathematical theorem- proving processes, we use Means and Ends Analysis.
The Disciplines of Artificial Intelligence
The subject of artificial intelligence spans a wide horizon. It deals with various kinds of knowledge representation schemes, different techniques of intelligent search, various methods for resolving uncertainty of data and knowledge, different schemes for automated machine learning and many others.
Among the application areas of AI, we have Expert systems, Game-playing, and Theorem-proving, Natural language processing, Image recognition, Robotics and many others. The subject of artificial intelligence has been enriched with a wide discipline of knowledge from Philosophy, Psychology, Cognitive Science, Computer Science, Mathematics and Engineering. Thus has the figure shows, they have been referred to as the parent disciplines of AI. An at-a-glance look at fig. also reveals the subject area of AI and its application areas.
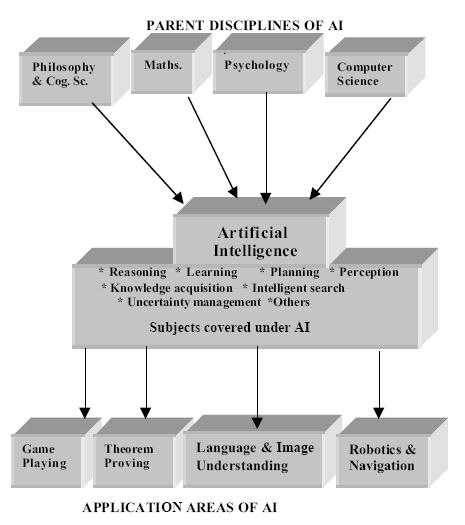
Fig.: AI, its parent disciplines and application areas.
The Subject of Artificial Intelligence
The subject of artificial intelligence was originated with game-playing and theorem-proving
programs and was gradually enriched with theories from a number of parent disciplines. As a young discipline of science, the significance of the topics
covered under the subject changes considerably with time. At present, the
topics which we find significant and worthwhile to understand the subject are
outlined below:
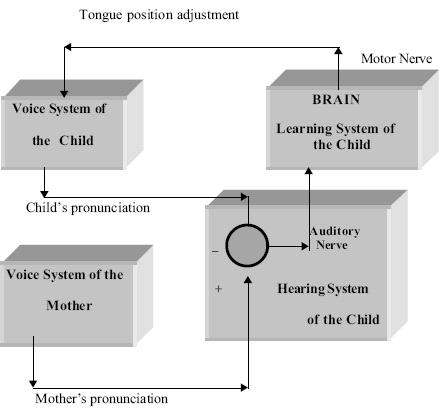
FigA: Pronunciation learning of a child from his mother.
Learning Systems: Among the subject areas covered under artificial intelligence, learning systems needs special mention. The concept of learning is illustrated here with reference to a natural problem of learning of pronunciation by a child from his mother (vide figA). The hearing system of the child receives the pronunciation of the character “A” and the voice system attempts to imitate it. The difference of the mother’s and the child’s pronunciation, hereafter called the error signal, is received by the child’s learning system auditory nerve, and an actuation signal is generated by the learning system through a motor nerve for adjustment of the pronunciation of the child. The adaptation of the child’s voice system is continued until the amplitude of the error signal is insignificantly low. Each time the voice system passes through an adaptation cycle, the resulting tongue position of the child for speaking “A” is saved by the learning process. The learning problem discussed above is an example of the well-known parametric learning, where the adaptive learning process adjusts the parameters of the child’s voice system autonomously to keep its response close enough to the “sample training pattern”. The artificial neural networks, which represent the electrical analogue of the biological nervous systems, are gaining importance for their increasing applications in supervised (parametric) learning problems. Besides this type, the other common learning methods, which we do unknowingly, are inductive and analogy-based learning. In inductive learning, the learner makes generalizations from examples. For instance, noting that “cuckoo flies”, “parrot flies” and “sparrow flies”, the learner generalizes that “birds fly”. On the other hand, in analogy-based learning, the learner, for example, learns the motion of electrons in an atom analogously from his knowledge of planetary motion in solar systems.
Knowledge Representation and Reasoning: In a reasoning problem, one has to reach a pre-defined goal state from one or more given initial states. So, the lesser the number of transitions for reaching the goal state, the higher the efficiency of the reasoning system. Increasing the efficiency of a reasoning system thus requires minimization of intermediate states, which indirectly calls for an organized and complete knowledge base. A complete and organized storehouse of knowledge needs minimum search to identify the appropriate knowledge at a given problem state and thus yields the right next state on the leading edge of the problem-solving process. Organization of knowledge, therefore, is of paramount importance in knowledge engineering. A variety of knowledge representation techniques are in use in Artificial Intelligence. Production rules, semantic nets, frames, filler and slots, and predicate logic are only a few to mention. The selection of a particular type of representational scheme of knowledge depends both on the nature of applications and the choice of users.
Planning: Another significant area of artificial intelligence is planning. The problems of reasoning and planning share many common issues, but have a basic difference that originates from their definitions. The reasoning problem is mainly concerned with the testing of the satisfiability of a goal from a given set of data and knowledge. The planning problem, on the other hand, deals with the determination of the methodology by which a successful goal can be achieved from the known initial states. Automated planning finds extensive applications in robotics and navigational problems, some of which will be discussed shortly.
Knowledge Acquisition: Acquisition (Elicitation) of knowledge is equally hard for machines as it is for human beings. It includes generation of new pieces of knowledge from given knowledge base, setting dynamic data structures for existing knowledge, learning knowledge from the environment and refinement of knowledge. Automated acquisition of knowledge by machine learning approach is an active area of current research in Artificial Intelligence. Intelligent Search: Search problems, which we generally encounter in Computer Science, are of a deterministic nature, i.e., the order of visiting the elements of the search space is known. For example, in depth first and breadth first search algorithms, one knows the sequence of visiting the nodes in a tree. However, search problems, which we will come across in AI, are non-deterministic and the order of visiting the elements in the search space is completely dependent on data sets. The diversity of the intelligent search algorithms will be discussed in detail later.
Logic Programming: For more than a century, mathematicians and logicians were used to designing various tools to represent logical statements by symbolic operators. One outgrowth of such attempts is propositional logic, which deals with a set of binary statements (propositions) connected by Boolean operators. The logic of propositions, which was gradually enriched to handle more complex situations of the real world, is called predicate logic. One classical variety of predicate logic-based programs is Logic Program. PROLOG, which is an abbreviation for PROgramming in LOGic, is a typical language that supports logic programs. Logic Programming has recently been identified as one of the prime area of research in AI. The ultimate aim of this research is to extend the PROLOG compiler to handle spatio-temporal models and support a parallel programming environment. Building architecture for PROLOG machines was a hot topic of the last decade.
Soft Computing: Soft computing, according to Prof. Zadeh, is “an emerging approach to computing, which parallels the remarkable ability of the human mind to reason and learn in an environment of uncertainty and imprecision” . It, in general, is a collection of computing tools and techniques, shared by closely related disciplines that include fuzzy logic, artificial neural nets, genetic algorithms, belief calculus, and some aspects of machine learning like inductive logic programming. These tools are used independently as well as jointly depending on the type of the domain of applications.
Management of Imprecision and Uncertainty: Data and knowledgebases in many typical AI problems, such as reasoning and planning, are often contaminated with various forms of incompleteness. The incompleteness of data, hereafter called imprecision, generally appears in the database for i) lack of appropriate data, and ii) poor authenticity level of the sources. The incompleteness of knowledge, often referred to as uncertainty, originates in the knowledge base due to lack of certainty of the pieces of knowledge Reasoning in the presence of imprecision of data and uncertainty of knowledge is a complex problem. Various tools and techniques have been devised for reasoning under incomplete data and knowledge. Some of these techniques employ i) stochastic ii) fuzzy and iii) belief network models. In a stochastic reasoning model, the system can have transition from one given state to a number of states, such that the sum of the probability of transition to the next states from the given state is strictly unity. In a fuzzy reasoning system, on the other hand, the sum of the membership value of transition from the given state to the next state may be greater than or equal to one. The belief network model updates the stochastic / fuzzy belief assigned to the facts embedded in the network until a condition of equilibrium is reached, following which there would be no more change in beliefs. Recently, fuzzy tools and techniques have been applied in a specialized belief network, called a fuzzy Petri net, for handling both imprecision of data and uncertainty of knowledge by a unified approach.
Applications of Artificial Intelligence Techniques
Almost every branch of science and engineering currently shares the tools and
techniques available in the domain of artificial intelligence. However, for the sake of the
convenience of the readers, we mention here a few typical applications, where
AI plays a significant and decisive role in engineering automation.
Expert Systems: In this example, we illustrate the reasoning process
involved in an expert system for a weather forecasting problem with special
emphasis to its architecture. An expert system consists of a knowledge base,
database and an inference engine for interpreting the database using the
knowledge supplied in the knowledge base. The reasoning process of a typical
illustrative expert system is described in Fig. PR 1 in Fig. represents
i-th production rule.
The inference engine attempts to match the antecedent clauses (IF parts)
of the rules with the data stored in the database. When all the antecedent
clauses of a rule are available in the database, the rule is fired, resulting in
new inferences. The resulting inferences are added to the database for
activating subsequent firing of other rules. In order to keep limited data in the
database, a few rules that contain an explicit consequent (THEN) clause to
delete specific data from the databases are employed in the knowledge base.
On firing of such rules, the unwanted data clauses as suggested by the rule are
deleted from the database.
Here PR1 fires as both of its antecedent clauses are present in the
database. On firing of PR1, the consequent clause “it-will-rain” will be added
to the database for subsequent firing of PR2.
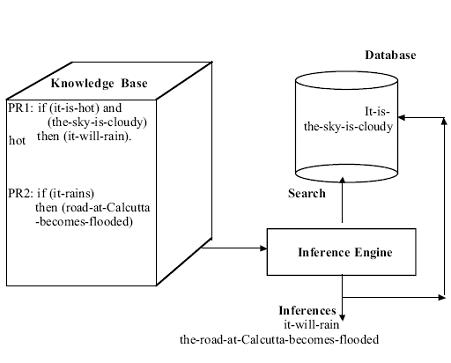
Fig. Illustrative architecture of an expert system.
Image Understanding and Computer Vision: A digital image
can be regarded as a two-dimensional array of pixels containing gray levels
corresponding to the intensity of the reflected illumination received by a
video camera. For interpretation of a scene, its image should be passed
through three basic processes: low, medium and high level vision .
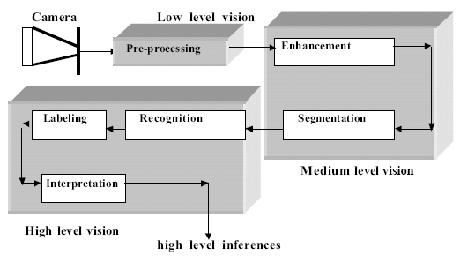
Fig.: Basic steps in scene interpretation.
The importance of low level vision is to pre-process the image by filtering from noise. The medium level vision system deals with enhancement of details and segmentation (i.e., partitioning the image into objects of interest ). The high level vision system includes three steps: recognition of the objects from the segmented image, labeling of the image and interpretation of the scene. Most of the AI tools and techniques are required in high level vision systems. Recognition of objects from its image can be carried out through a process of pattern classification, which at present is realized by supervised learning algorithms. The interpretation process, on the other hand, requires knowledge-based computation.
Speech and Natural Language Understanding: Understanding of speech and natural languages is basically two class ical problems. In speech analysis, the main probl em is to separate the syllables of a spoken word and determine features like ampli tude, and fundamental and harmonic frequencies of each syllable. The words then could be ident ified from the extracted features by pattern class ification techniques. Recently, artificial neural networks have been employed to class ify words from their features. The probl em of understanding natural languages like English, on the other hand, includes syntactic and semantic interpretation of the words in a sentence, and sentences in a paragraph. The syntactic steps are required to analyze the sentences by its grammar and are similar with the steps of compilation. The semantic analysis, which is performed following the syntactic analysis, determines the meaning of the sentences from the association of the words and that of a paragraph from the closeness of the sentences. A robot capable of understanding speech in a natural language will be of immense importance, for it could execute any task verbally communicated to it. The phonetic typewriter, which prints the words pronounced by a person, is another recent invention where speech understanding is employed in a commercial application.
Scheduling: In a scheduling problem, one has to plan the time schedule of
a set of events to improve the time efficiency of the solution. For instance in
a class-routine scheduling problem, the teachers are allocated to different
classrooms at different time slots, and we want most classrooms to be
occupied most of the time. In a flowshop scheduling problem, a set of
jobs J1 and J2 (say) are to be allocated to a set of machines M1, M2 and M3.
(say). We assume that each job requires some operations to be done on all
these machines in a fixed order say, M1, M2 and M3. Now, what should be
the schedule of the jobs (J1-J2) or (J2 -J1), so that the completion time of both
the jobs, called the make-span, is minimized? Let the processing time of jobs
J1 and J2 on machines M1, M2 and M3 be (5, 8, 7) and (8, 2, 3) respectively.
The gantt charts in fig. (a) and (b) describe the make-spans for the
schedule of jobs J1 - J2 and J2 - J1 respectively. It is clear from these figures
that J1-J2 schedule requires less make-span and is thus preferred.
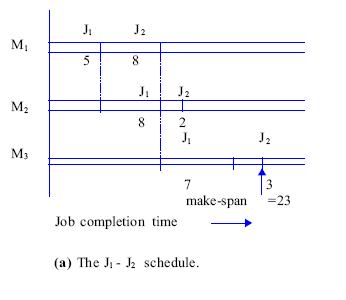
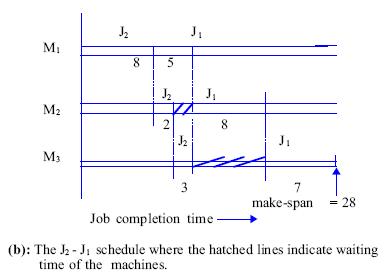
Fig.: The Gantt charts for the flowshop scheduling problem
with 2 jobs and 3 machines.
Flowshop scheduling problems are a NP complete problem and determination of optimal scheduling (for minimizing the make-span) thus requires an exponential order of time with respect to both machine-size and job-size. Finding a sub-optimal solution is thus preferred for such scheduling problems. Recently, artificial neural nets and genetic algorithms have been employed to solve this problem. The heuristic search, to be discussed shortly, has also been used for handling this problem.
Intelligent Control: In process control, the controller is designed from the
known models of the process and the required control objective. When the
dynamics of the plant is not completely known, the existing techniques for
controller design no longer remain valid. Rule-based control is appropriate in
such situations. In a rule-based control system, the controller is realized by a
set of production rules intuitively set by an expert control engineer. The
antecedent (premise) part of the rules in a rule-based system is searched
against the dynamic response of the plant parameters. The rule whose
antecedent part matches with the plant response is selected and fired. When
more than one rule is firable, the controller resolves the conflict by a set of
strategies. On the other hand, there exist situations when the antecedent part
of no rules exactly matches with the plant responses. Such situations are
handled with fuzzy logic, which is capable of matching the antecedent parts of
rules partially/ approximately with the dynamic plant responses. Fuzzy control has been successfully used in many industrial plants. One typical
application is the power control in a nuclear reactor. Besides design of the
controller, the other issue in process control is to design a plant (process)
estimator, which attempts to follow the response of the actual plant, when
both the plant and the estimator are jointly excited by a common input signal.
The fuzzy and artificial neural network-based learning techniques have recently
been identified as new tools for plant estimation.
